CBPS and Entropy Balancing: Simulation Study

Introduction:

A key challenge in the application of propensity scores for matching is that the propensity score is unknown and must be estimated. To make matters worse, slight misspecification of the propensity score model can lead to substantial biases in treatment effects. This has led to researchers iteratively re-estimating the propensity score model, subsequently checking the resulting covariate balance, then repeating over and over until they are satisﬁed. Imai et al (2008) calls this the ‘propensity score tautology’: the estimated propensity score is appropriate if it balances covariates.

In this simulation study, I analyze two approaches that seek to bypass this ‘propensity score tautology’: Covariate Balancing Propensity Score and Entropy Balancing. Each method obviates the need for iteratively re-estimating the propensity score model and checking balance on the covariate moments. That is, a single model is used to estimate both the treatment assignment mechanism and the covariate balancing weights.

Matching and Propensity Scores:

In an observational study setting where the confounding covariates (variables correlated with both treatment and outcome) are known and measured, we may use matching methods to ensure that there is sufficient overlap and balance on these covariates. Then, we can estimate the treatment effect using a simple difference in means or regression methods.

Overlap is important because we want to make sure that for each treated or control subject in the study, there exists an empirical counterfactual (this criteria varies depending on the estimand of interest, i.e. to estimate the ATT it is sufficient to have empirical counterfactuals for just the treated subjects in the study). Balance on the covariates is important because imbalance would force us to rely more on the correct functional form of the model.

There are many different matching methods, but the driving principle is to identify observations that are “most similar”, based on some distance metric. Methods include K-nearest-neighbor, caliper-matching, kernel-matching, Mahalanobis matching, Genetic Matching, Optimal Matching.

A propensity score is a one-number summary of the covariates. Rosenbaum and Rubin (1983) define the propensity score for participant i as the conditional probability of treatment assignment ( $Z_i = 1$ ) given a vector of observed covariates: $e(X i ) = Pr(Z i = 1|X)$ . The most common traditional approaches to estimating the propensity score are logistic regression and probit regression.

If strong ignorability holds after conditioning on the propensity score, that is:

$y_{0},y_{1}\ \bot\ Z_{i}|e(X_{i}),\ 0 < e(X_{i}) < 1$

Then we may obtain an unbiased estimate of the treatment effect by either matching or weighting using just the propensity score instead of the vector of covariates.

After using either matching, propensity scores, or both to obtain a subset of the data that exhibits sufficient overlap, simple mean differences or a linear regression using weights can be used to estimate the treatment effect (ATE, ATC, or ATT). In all cases, ignorability, sufficient overlap, appropriate specification of the propensity score model / good balance, and SUTVA are all important assumptions to obtain unbiased estimates of the treatment effect. The Stable Unit Treatment Value Assumption (SUTVA) states that the potential outcomes are independent of the particular configuration of treatment assignment. That is, there are no diluting or concentrating effects.

To summarize assumptions, propensity score and matching methods require that the structural assumptions of ignorability and SUTVA are met. And to a lesser degree make parametric assumptions: correct specification of the propensity score model. Theoretically, in some cases, sufficient overlap and balance may make the outcome estimation model robust to misspecification and thereby helps to relax the parametric assumptions.

Covariate Balancing Propensity Score (CBPS):

The CBPS exploits the dual characteristics of the propensity score as a covariate balancing score and the conditional probability of treatment assignment (Imai and Ratkovic (2012))

First, consider a commonly used model for estimating propensity scores: logistic regression (point of this part is to show the dual characteristics!):

$e_{B}(X_{i}) = \frac{exp(X_{i}^{T}\beta)}{1+exp(X_{i}^{T}\beta)}$

We typically estimate the unknown parameters by maximum likelihood:

$\hat{\beta}_{MLE} = \arg \max_{\beta} \sum_{i=1}^{N}Z_{i}\ log\{e_{B}(X_{i})\ + (1-Z_{i})\ log\{1-e_{B}(X_{i})\}$

And we get the ML estimates by differentiating the log likelihood with respect to the parameters then setting the derivative to zero. So differentiating with respect to $\beta$ , we get:

$\frac{1}{N}\sum_{i=1}^{N} \frac{Z_i\ e'_{B}(X_{i})}{e_{B}(X_{i})} - \frac{(1-Z_i)\ e'_{B}(X_{i})}{1-e_{B}(X_{i})}$

Then, they operationalize the covariate balancing property by using inverse propensity score weighting:

$E\left\{ \frac{Z_i\ \tilde{X_{i}}}{e_{B}(X_{i})} - \frac{(1-Z_i)\tilde{X_{i}}}{1-e_{B}(X_{i})} \right\} = 0$

where $\tilde{X_i} = f(X_i)$ , a function of $X_i$ specified by the researcher. Which happens to look a lot like the difference between treatment weights and control weights under inverse propensity score weighting (IPSW)! (If we substitute $Y_i$ for $\tilde{X_i}$ , we get exactly the difference between the inverse propensity score weighted treated and control outcomes.) The inverse propensity score weights are used to make the treated group “look like” the control group. And here, the weighting provides a condition that balances a particular function of covariates (i.e. the mean or variance). Setting $\tilde{X_i} = e'_{B}(X_{i})$ gives more weights to covariates that are predictive of treatmeent assignment according to the logistic regression propensity score model. But so long as the expectaion exists, the equation must hold for any choice of f(.). For example, setting $\tilde{X_i} = X_i$ ensures the first moment of each covariate is balanced. Setting $\tilde{X_i} = (X_{i}^TX_i^{2T})^T$ ensures the first and second moment of each covariate is balanced. Hence, we’ve established the “dual” characteristics of the propensity score as a covariate balancing score and conditional probability of assignment.

To estimate the CBPS, Imai uses the GMM or EL framework. For more details please see Imai and Ratkovic (2014).

Entropy Balancing:

Entropy balancing similarly involves a reweighting scheme that directly incorporates covariate balance into the weight function (Heinmueller 2015). To do this, entropy balancing searches for a set of weights that satisfies the balance constraints, while trying to keep the distribution of weights as uniform as possible (i.e. minimizing the divergence of distribution of weights from a uniform distribution). Thus, entropy balancing (1) allows us to obtain a high degree of covariate balance (using balance constraints that can involve the first, second, and possibly higher moments of the covariate distributions as well as interactions). And (2) allows for a more flexible reweighting scheme that seeks to retain as much information as possible. For example, nearest neighbor matching may discard subjects that are not matched (i.e. set weight equal to 0).

Consider the reweighting scheme to estimate the Average Treatment Effect on the Treated (ATT). We would want to estimate the counterfactual mean by:

$E[\widehat{Y(0)|Z=1}] = \frac{\sum_{i|Z=0}Y_iw_i}{\sum_{i|Z=0}w_i}$

where $w_i$ is a weight for each control unit.

The weights are chosen by the following reweighting scheme:

$H(w) = \sum_{i|D=0}h(w_i)$
where $h(.)$ is a distance metric and $c_{ri}(X_i) = m_r$ describes a set of R balance constraints imposed on the covariate moments of the reweighted control group.

Minimize $H(w)$ subject to the balance and normalizing constraints:

$\sum_{i|D=0} w_ic_{ri}(X_i) = m_r$

with $r$ $\in$ $1,..., r$

$\sum_{i|Z=0}w_i = 1$

and $w_i \geq 0$ for all $i$ such that $T = 0$ .

Comparison and Implementation:

Both methods may be used to estimate either the ATT, ATC, or the ATT, and the two methods are very similar. The key difference is that entropy balancing bypasses the ‘propensity score tautology’ by ignoring the propensity score model estimation step. Instead, it looks for weights that achieve the best balance, subject to a constraint that seeks to retain as much information in the data as possible. In contrast, covariate balancing directly exploits the dual characteristic to estimate propensity scores AND balance covariates simultaneously.

For implementation, I use the ‘ebal’ and ‘CBPS’ packages in R to implement Entropy Balancing and Covariate Balancing Propensity Score, respectively.

Simulation Set Up:

Features:

In this section, I examine whether the CBPS or Entropy Balancing methods improve upon the performance of baseline approaches to both (1) achieving balanced covariates and (2) estimating the treatment effect. The baseline approach estimates include (1) propensity scores using logistic regression and matches using 1-1 matching with replacement and (2) mahalanobis matching with replacement.

Though ignorability may be the most crucial assumption, I assume that all of the confounders are known to the researcher for all simulations. I believe that testing the sensitivity to the ignorability assumption would be more interesting when comparing propensity score and matching methods to other causal inference models. Since the authors of CBPS and EB claim that these models are less dependent on correctly specification compared to traditional propensity score approaches, I’m most interested in:

reliance on the correct specification of the propensity score model
reliance on the correct specification of the outcome model
reliance on the ellipsoidally symmetric shape of covariate distributions

It’s clear from earlier discussion why reliance on correct specification is important. I add feature (3) because Mahalanobis distance and propensity score matching may make balance worse if the covariates are not EPBR (equal percent bias reducing). But both methods are equal percent bias reducing if all of the covariates used have ellipsoidal distributions (e.g. multivariate normal).

Estimand:

The estimand of interest is the ATT: Average Effect of Treatment on the Treated. The ATT tells us how much the treatment affected the group of subjects that receieved treatment. We estimate the ATT by comparing the observed outcomes to the counterfactual outcomes that we would have measured had this group of subjects not received treatment. But since we are not able to observe this counterfactual state, we match each of these treated individuals to a control subject.

Data Generating Process:

I consider four data generating processes:

Standard Normally Distributed Covariates: The pre-treatment covariates $X_i = (X_{i1},X_{i2},X_{i3},X_{i4})$ are four independent and identically distributed random variables following a standard normal distribution. The true propensity score model is a logistic regression whose linear predictor is a linear transform of the pre-treatment covariates.
Standard Normally Distributed Covariates (non-linear propensity score model): The pre-treatment covariates are the same as Simulation #1; however, the true propensity score model is a logistic regression whose linear predictor are non-linear transforms of the pre-treatment covariates: $X_i^* = (-exp(X_{i1}/2), - X_{i2}/(1+exp(X_{i1})), X_{i3}, - sqrt(X_{i4}^2))$
Standard Normally Distributed Covariates + 3 count covariates: The pre-treatment covariates $X_i = (X_{i1},X_{i2},X_{i3},X_{i4},X_{i5},X_{i6},X_{i7})$ consist of four independent and identically distributed random variables following a standard normal distribution, a random variable following a poisson distribution with $\lambda = 1$ , the negative values of a random variable following a binomial distribution with $n = 3$ and $p = 0.8$ , and a random variable following a chi-squared distribution with $df = 1$ .
Standard Normally Distributed Covariates + 3 count covariates (non-linear propensity score model): The pre-treatment covariates are the same as Simulation (5); however, the true propensity score model is a logistic regression whose linear predictor are non-linear transforms of the pre-treatment covariates: $X_i^* = (0.5*exp(X_{i1}/2),\ X_{i2}/(1+exp(X_{i1})),\ -.2*X_{i3}^2,\ X_{i1}*X_{i4},\ -0.4*sqrt(X_{i5}-X_{i6}),\ 0.2*(X_{i1}+1.2*X_{i6})^2,\ 0.5*X_{i7})$

I run each DGP twice, for a total of 8 simulations. For the first set of four simulations, the true outcome model is a linear regression with the pre-treatment covariates as predictors. For the second set of four simulations, the true outcome model is a linear regression with non-linear transformations of the pre-treatment covariates as predictors. I use the following non-linear model:

$y_i = x_1^2 + x_1x_2 + x_3^2 + \sqrt{x_4}$

Matching Methods:

Here, I briefly review the baseline models, then the specific specifications of the CBPS and EB models used in this simulation. For all six methods, the target estimand is the ATT and I match accordingly (that is, treated subjects receive weights equal to one and control subjects receive adjusted weights).

Baseline: Propensity Score using Logistic Regression:
Baseline: Mahalanobis Matching
CBPS (1)
CBPS (2)
EB (1)
EB (2)

The first baseline model uses logistic regression (without any interactions or transformations) to estimate propensity scores. I match using 1-1 nearest neighbor matching using the propensity scores.

The second baseline model uses Mahalanobis matching. Mahalanobis calculates distance as $m^2 = (x_T - x_C)'\Sigma_{CR}^{-1}(x_t-x_C)$ and it is equivalent to Euclidean matching based on standardized and orthogonalized X. To estimate the ATT: for each treatment subject, I match with replacement the control subject with the smallest Mahalanobis distance. Mahalanobis was intended for use with multivariate normally distributed data. When some covariates exhibit extreme outliers or very skewed distributions, Mahalanobis distance will place less weight on that covariate. On the other hand, a binary variable with a .99 probability of one would have low standard deviation and the Mahalanobis distance would give greater weight to this variable. One way to address these concerns would be to use a rank-based Mahalanobis distance. For this simulation study, I use the standard Mahalanobis distance.

The third and fourth models use CBPS: an over-identified model and a just-identified model. The over-identified model (#3) combines the propensity score AND covariate balancing conditions. The just-identified model (#4) only contains covariate balancing conditions.

The fifth and sixth models use Entropy Balancing: one that achieves balance on just the first moment (#5) and one that achieves balance on both first and second moments (#6).

For all 6 models, I use a linear regression using (1) weights to reflect the restricted dataset of the corresponding matching method and (2) all observed covariates (without any interactions or transformations) to estimate the ATT.

Simulations:

ps densities

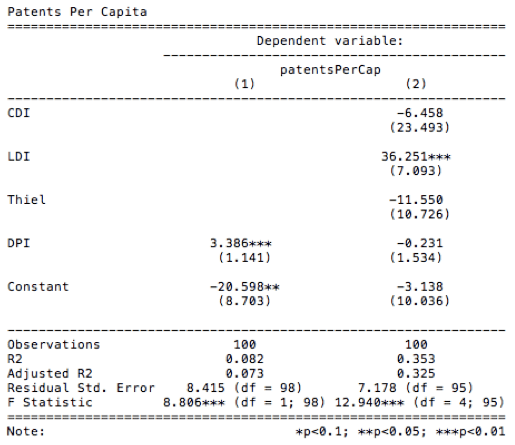
The above plots show the density of the true propensity score in treatment and control groups for each simulation. There is a misleading pattern: the linear propensity score models (#1 and #3) have strong separation, whereas the non-linear propensity score models (#2 and #4) show a platykurtic treatment distribution with positively skewed control density. However, this is totally arbitrary and is reflective of the specification of the true propensity score model. But this is ok because I’m interested in comparing the relative performances of the models given a simulation.

Examine Overlap of Propensity Score and Covariates (Before Matching):

md1 md2

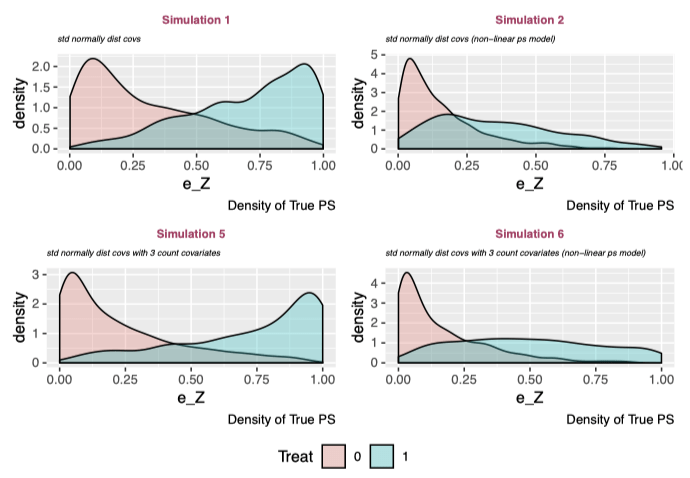
Analysis of Mean Differences:

Entropy balancing shows the best performance with respect to balancing covariate means. For all 4 simulations, the standardized mean difference is approximately zero for all covariates.
The CBPS just-identified model similarly achieves perfectly balanced covariate means.
The CBPS over-identified model performs significantly better in simulations where the true propensity score model is non-linear and worse in simulations where the true propensity score model is linear, which seems counter-intuitive. In fact, for both simulations with a non-linear true propensity score model, the CBPS over-identified model achieves nearly 0 mean difference for all covariates, where as mean differences remain large for both simulations with linear true propensity score model. One observation is that when the true propensity score model is linear, the covariates’ mean differences are similar to the covariates’ mean differences under the logistic model. Recall that the over-identified model combines the propensity score and covariate balancing conditions whereas the just-identified model only contains covariate balancing conditions. It seems likely that when the true propensity score model is linear in the covariates, the propensity score condition “dominates” the covariate balancing conditions, so the CBPS over-identified model’s performance resembles the logistic baseline model’s results. For the simulations with a non-linear propensity score model, the propensity score condition no longer dominates, so the CBPS over-identified model’s performance resembles the just-identified model’s results.
The logistic regression and mahalanobis matching methods show strong performance in simulation 1, where the pre-treatment covariates have standard normal distributions. Performance appears to weaken after including count variables and when the true propensity score model is non-linear.

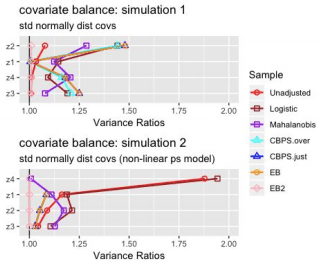
Analysis of Variance Ratios:

The Entropy Balancing model where I have set both first and second moment conditions (EB 2) is the only model that consistently achieves variance ratios = 1. The other models’ ability to obtain similar variances of matched samples across treatment groups is rather sporadic.

Results:

Below, the first three tables display results from the 4 simulations for which the true outcome model is linear. The latter three tables show the equivalent results, except with a non-linear true outcome model. I also plot these tables so that it’s easier to visually inspect model results across simulations.

Caution: we should only compare models (columns) given a row (simulation). For example, based on Table 3, it is incorrect to claim that “Simulation #2 (multivariate normal covariates with misspecified propensity score model) has lower RMSE than Simulation #1 (multivariate normal covariates with correctly specified propensity score model)”. This result can quickly be reversed by changing the specification of the true propensity score model. Rather, we are interested in how the models’ performances (e.g. CBPS 1 vs EB-1) given a simulation.

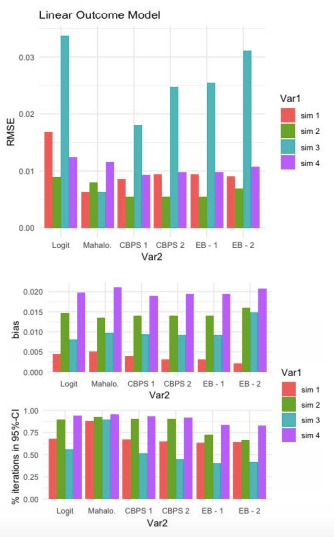
Linear Outcome Model:

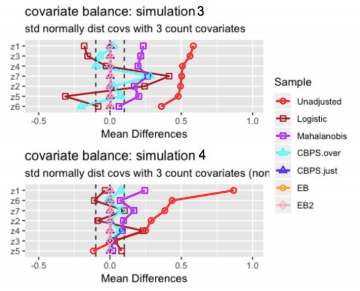
For this first set of simulations, Mahalanobis has the lowest RMSE for 2 out of 4 simulations. Both of these simulations have a linear true propensity score model. When the true propensity score model is non-linear (#2 and #4), Mahalanobis does better than Logit but worse than CBPS and EB.

All models do better than the baseline logit model (keeping in mind that this baseline model made no attempt to improve the propensity score estimation model).

Comparing CBPS and EB, the over-identified CBPS model (CBPS 1) either ties or out-performs the other specifications of CBPS and EB. CBPS does better when it exploits the dual specification (over-identified) than when it solely balances covariates (just-identified).

As cautioned above, these plots do not suggest that CBPS and EB models underperform for Simulation #3. Simulation #3 is equivalent to #4, except that the true propensity score model is LINEAR for #3 and NON-LINEAR for #4. So the expectation (all else equal) would be that the models would perform better when the true propensity score model is linear. But all else is NOT equal, the DGP (i.e. distributions of the true propensity scores) differ across simulations.

The third graph shows the percentage of iterations in which the true SATT (Sample Average Treatment Estimate on the Treated) falls inside the 95% confidence interval of estimated SATT. These results are much more discouraging for CBPS and EB. They appear to trivially improve upon the baseline logit model (if at all) and for simulations #1 and #3, perform much worse than the Mahalanobis estimate.

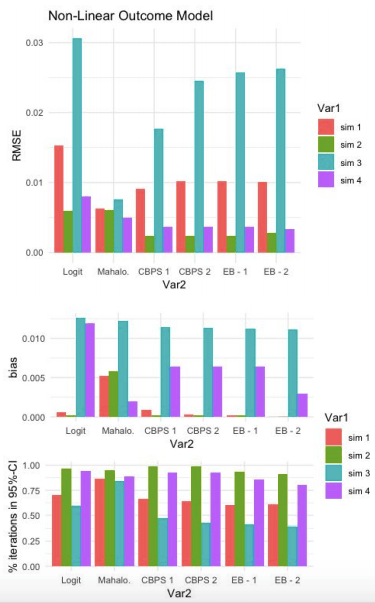
Non-Linear Outcome Model:

Comparison of RMSE results in the same patterns as the Linear-Outcome case above. Mahalanobis does better the other models when the true propensity score model is linear. With a non-linear true propensity score model, CBPS and EB both achiever lower RMSE than Logit and Mahalanobis. Once again, the CBPS-1 model does at least as well as any of the other CBPS or EB models.

Similar to the previous result, CPBS and EB do not appear to do much better than Logit with respect to % of iterations capturing true SATT within a 95% confidence interval of estimated SATT.

nlo1 nlo2

References:

Diamond, A. and Sekhon, J. 2012. Genetic matching for estimating causal effects: a new method of achieving balance in observational studies.
Hainmueller, Jens. 2012. “Entropy Balancing for Causal Effects: A Multivariate Reweighting Method to Produce Balanced Samples in Observational Studies.” Political Analysis 20(1): 25–46.
Imai, K., King, G. and Stuart, E. A. 2008. Misunderstandings between experimentalists and observationalists about causal inference. J. R. Statist. Soc. A, 171, 481–502.
Imai, Kosuke, and Marc Ratkovic. 2014. “Covariate Balancing Propensity Score.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 76(1): 243–63.
Rosenbaum, Paul R. and Donald B. Rubin. 1983. “The Central Role of the Propensity Score in Observational Studies for Causal Effects.” Biometrika 70 (1): 41–55.
Rubin, Donald B. 1976a. “Multivariate Matching Methods That are Equal Percent Bias Reducing, I: Some Examples.” Biometrics 32 (1): 109–120.

Spatial Analysis of Hot Spot Policing using Stop-and-Frisk (SQF)

Collaborative Project with Karen Cao (NYU MS Applied Statistics), Tana Wuren (NYU MS Applied Statistics), and Tina Koo (NYU MPH Global Health)

Introduction:

Definition of Hot Spots: Police departments frequently concentrate efforts in high crime areas. For example, under Operation Impact, the New York Police Department (NYPD) deployed additional officers into “Impact Zones”, neighborhoods with historically high patterns of crime. Similarly, a quick glance at data shows clear regions where NYPD focused Stop-Question-and-Frisk (SQF) efforts, and we define these areas as hot spots.

Objective: The primary objective of our study is to evaluate the effectiveness of hot spot policing by assessing the hit rate of the area with the highest number of stops, where:

$hit\_rate = \frac{\#\ of\ stops\ with\ contraband\ found}{total\ \#\ of\ stops}$

Data: For this project, we restrict our analysis to 2013. From 2012 to 2013, there was a 64% decrease in the number of stops (from 532,911 to 191,851). If the policy appears to be ineffective after such a rapid drop in the number of stops, it was most likely ineffective prior to the drop as well.

Theory: Define a “threshold” as the level of reasonable suspicion required for an officer to conduct a search. Then the hit rate at a region i depends on $threshold_i$ and $p(hit_i)$ .

In a high crime area, there is a higher probability of a hit, $p(hit)$ , so we would expect that NYPD stop more people carrying weapons or contraband. On the other hand, an officer may have a lower threshold in a high crime area. Thus, an officer may stop individuals in a high crime area who otherwise may not have been stopped in a low crime area. For these individuals, the probability of a hit would be low even though the stop was conducted in a high crime neighborhood.

Given two sets of stops that are conducted in some neighborhoods, suppose that the only difference between the two sets is that one set of stops was conducted with high geographic concentration while the other was conducted with low concentration. In other words, one set of stops is is more clustered and the other is more dispersed. Then if hot spot policing is effective, we would expect to see a higher hit rate within the high concentration set.

theory_diagram_2

Methods and Results

To evaluate effectiveness, we compare the hit rate of the area with the highest number of stops with the overall hit rate distribution. We argue that if we discover a statistically higher hit rate in the area with the highest number of stops, despite potential lower standard for ‘reasonable suspicion’, there is compelling evidence that hot spot policing is effective. Alternatively, substantially lower hit rate suggests the need for further investigation to determine the effectiveness of SQF.

Step 1: Identifying area with the most SQF stops

First we identify spatial location at which a single circle with fixed radius of 0.01 contains the highest number of stops. We calculate the hit rate of the circle by dividing the number of hits by the total number of stops, and define this circle as our high-concentration circle.

Step 2: Testing for statistical significance

We take three simulation approaches to analyze whether the hit rate in our high-concentrated circle is significantly different from hit rates in other areas in NYC.

Approach 1: Fixed Radius Approach

Our first approach is to randomly select 1,000 stops as centroids and calculate the hit rates within each circle using the same radius of 0.01, which are represented by the blue circles in Figure 1. We generate the sampling distribution of the hit rate of the blue circles (blue distribution) and compare its mean to the hit rate of the high-concentrated circle (red dotted line). As the figure illustrates, the hit rate of the high-concentrated circle is lower than the mean of the sampling distribution of the 1,000 random sampled circles.

We also sample 1,000 stops from the entire area to estimate the expected distribution of hit rates under complete spatial randomness (green distribution). The mean of the blue distribution is the same as the mean of the green distribution (~0.04). However, the variance of the blue distribution is wider than that of the green due to spatial autocorrelation.

approach1

Approach 2: Fixed Stops Approach

Our second approach takes the population density into account by fixing the total number of stops. We randomly select 1,000 points as centroids from all five boroughs, draw circles around them and increase radius of each circle until each of them contains the same number of stops as the high-concentrated circle (approximately 7,000 stops). We calculate hit rate of each circle and obtain a sampling distribution (blue distribution). As shown in Figure 2, the red circle is still the high-concentrated circle, and the blue circle is one of the 1,000 circles whose centroid has been randomly selected and contains approximately 7,000 stops.

Based on the sampling distribution of hit rates in Figure 2, hit rate of the high-concentration area is still lower than that of the sampling distribution and the true mean hit rate of the entire area (~0.04). Compared to the sampling distribution obtained from the fixed radius approach, the sampling distribution obtained here has a narrower range, because we are less likely to get extreme hit rate outliers with a fixed number of stops in each circle.

approach2

Approach 3: “Doughnut” Approach

Our last approach takes demographic and geographic characteristics into consideration. We assume areas that are very close to each other share similar demographic and geographic characteristics. Under this assumption, we draw circles around the high-concentrated area and call them the Doughnut areas. Since they are very close to the high-concentrated circle, we assume that they share similar demographic and geographic characteristics.

As shown in Figure 3, we draw an orange circle outside the high-concentrated circle, and we make sure that there are approximately 7,000 stops within that orange circle but outside the red circle. Similarly, we then draw a bigger yellow circle and make sure that there are still approximately 7,000 stops within that yellow circle but outside the orange circle. Now we have three areas with the same number of stops (approximately 7,000): the red high-concentrated circle, the orange doughnut area, and the yellow doughnut area. Since we assume these areas to have similar demographic and geographic characteristics, we expect them to have similar hit rates. However, hit rate of the red high-concentrated circle is much lower than that of the other two doughnut areas: the red circle has a hit rate of 0.017, the orange doughnut area has a hit rate of 0.041, and the yellow doughnut area has a hit rate of 0.032. This could be a piece of evidence showing NYPD police officers are not conducting SQF effectively, as they conducted the most number of stops within the red circle but yielded the lowest hit rate among the three areas.

approach3

Conclusion

Using scan statistics, we were able to identify five circular areas within each borough with the most SQF stops. The results of our three spatial analytic approaches indicate that the hit rate of the area with the most SQF stops in 2013 was significantly lower than the mean hit rate of other areas. This suggests a need for further investigation into whether the NYPD is using its resources effectively.

Limitations

A major limitation of our analysis was our inability to consider the counter argument that the lower hit rates in areas with a higher frequency of stops is evidence of the efficacy of hot spot policing. Essentially, some claim that targeting high crime neighborhoods with increased surveillance and threat of being stopped discourages individuals from carrying weapons and contrabands. It is also possible that people who are likely to carry weapons or contrabands become aware of and avoid areas with higher likelihood of being stopped. In addition, our study likely underestimates the actual number of stops in each neighborhood due to inaccurate or incomplete reporting by officers.

When determining the high-concentration circle, we didn’t account for bodies of water, parks, cemeteries, or other areas without people. It is also possible that the area with the highest concentration of stops represents an outlier; therefore our results may not be generalizable. An alternative approach we could have taken is to create a sampling distribution of 10% of identified hot spots. In our third approach, we use the doughnut method to compare the hit rate in nearby areas with comparable demographic and neighborhood characteristics. However, this method is limited because it assumes isotropy. Instead of this approach, we could have used random points on the border of the high-concentration circle as centroids to create a Spirograph. This may have resulted in larger areas with more similar characteristics and better approximated the sampling distribution of neighbors.

Code and Data

Our code is available on the github repository (https://github.com/chansooligans/spatial_project).

Main code: The file “Spatial_Project.Rmd” is the master code.
Shiny Apps: Each of the “Spatial_Shiny_App” folders contain a .R file. These are the R Shiny Apps that were used to demonstrate simulations. Simply open then click “Run” to run the app.
Code to Identify Circles with Highest Concentration: To identify circles with highest concentration, I had to compute very large distance matrices. In order to use the HPC Clusters, separate .R files were created: “parallel_dist_spacial.R” and “parallel_dist_spacial_bk.R”. A separate script was used for Brooklyn because Brooklyn has many stops.

Heterogeneity in Perspectives and Entrepreneurship: Regional Analysis of the United States

Introduction

In an increasingly integrated society, heterogeneity of worldview is growing in nearly all advanced economies. According to the Center for Immigration Studies, the foreign-born population in the United States hit 42.4 million, or 13.3 percent, of the total US population in 2014. With easy access to the Internet, ideas can spread rapidly allowing scholars to virtually coordinate research with labs across continents and religious missionaries to proselytize tens of thousands in all corners of the world. The previous literature on international economic development asserts that ethnic and religious fractionalization can reduce support for public goods, generate communication costs, and induce divisiveness. Other studies on diversity note that heterogeneity also widens the pool of knowledge and variety of preference sets, increasing the breadth of goods, services, and ideas available for consumption and production. To contribute to the literature on the economic effects of diversity, the objective of this paper is to examine the relationship between worldview diversity and entrepreneurial activity in US metropolitan areas.

I make three contributions in this paper. First, I construct and assess a new index of worldview diversity, called the Diversity of Perspectives Index (DPI), which defines each combination of nationality, gender, field of study, and occupation as a unique identity. It differs from previous studies analyzing political and economic effects of diversity, which rely on either ethnicity, language, or religion to define cultural identity. Unlike these traditional measures of diversity, the DPI better captures the integration and assimilation of various cultures. Further, the DPI places equivalent weights on the value of ethnic, linguistic, gender, academic, and occupational diversity. Second, I investigate the relationship between this newly constructed index, the DPI, and startup formation using an OLS linear regression model. Last, I incorporate previously used diversity indices into the model to test the strength of the DPI as an indicator of startup activity relative to simpler measures of cultural diversity. The regression results of DPI on new firms per 10000 capita reveal a statistically significant relationship. The significance of the DPI’s effect on startup formation withstands the addition of other indices to the model.

Diversity at the Firm Level:

A diverse environment contains a greater number of perspectives than a more homogenous society. With a greater variety of approaches to solving problems, there is an increased likelihood of an optimal solution as well as an increased likelihood of conflicting opinions. Both outcomes increase incentives for the founding of new firms whether the motive is to exploit a business opportunity or to challenge an established business with a conflicting and unique idea. Previous literature has studied this relationship and the mechanisms facilitating the relationship between diversity and productivity on both the firm and societal levels.

At the firm level, Hong and Page (2001) decompose the effect of heterogeneity in problem solving behavior by identifying (1) how people perceive problems internally, their “perspectives”, and (2) how they go about solving them, their “heuristics”. They show theoretically that all else equal, e.g. absence of incentive and communication problems, less-skilled groups with diverse perspectives or heuristics can outperform relatively more skilled groups that are homogenous. The contention that greater variety in heuristics and perspectives leads to better outcomes may seem noncontroversial. Nevertheless, the formal model contributes a useful tool for economists to understand the mechanisms driving productivity in the presence of diversity.

In a separate study, Hong and Page (2004) extend the cognitive benefits of a diverse environment to show that even randomness, given a diverse pool of intelligent people, can assemble a group that outperforms a group of top scorers. They provide an illustrative example in which an organization administers a test to 1000 individuals with the aim of hiring a team to solve a difficult problem. Their conclusion asserts a randomly selected group can outperform top performers as long as certain criteria are met. For example, if the pool of individuals is large enough, the group of top performers is likely to be more homogenous since the test funnels like-minded individuals to the top. However, if the group is too large, the group of top scorers may itself become diverse and perform relatively better. Therefore, the advantage of random selection over performance-based selection faces decreasing marginal returns commensurate to the size of the group. When considering the real-world applicability of this study’s theoretical findings, one key limitation is the absence of communication costs that would surely arise with teams whose members speak different languages.

By observing firm-level impacts of cultural heterogeneity as measured by linguistic diversity, Edward Lazear (1999) addresses this concern. In his model, there is a possibility of individuals speaking different languages. According to his findings, firms that combine cultures incur costs because some team members must be bilingual or bicultural. However, cross-cultural interactions can increase overall productivity through increase in variety of skills available and strategic complementarities from disparate information sets. Given a profit-maximizing objective and a production unit, there exists an optimal level of heterogeneity where the benefits of diversity outweigh its communication costs.

Jehn, Northcraft, and Neale (1999) distinguish several types of diversity, such as social category diversity and value diversity. Social category diversity is defined by explicit differences in social category membership, namely race, gender, and ethnicity. Value diversity occurs when members of a workgroup differ in terms of what they think the group’s real task, goal, target, or mission should be. The study finds that social category diversity positively influences group member morale, while value diversity decreases satisfaction, intent to remain, and commitment to the group.

These studies show that diversity benefits groups by widening the range of viewpoints, but can also introduce costs. However, the merits of diversity can be codependent on the costs themselves. Through debate and challenges of each others’ assumptions, the adversarial environment gives rise to optimal solutions. So the effect of diversity and whether its benefits can be fully realized largely depends on the group’s ability cooperate. At the firm level, it is possible that a united profit-maximizing orientation can mitigate the harmful potential of diversity.

Political and Social Effects of Diversity:

On a societal level, a greater number of individuals as well as a greater number of distinct ideological viewpoints can increase both coordination costs as well as the potential for conflict. This suggests that the benefits of diversity within groups at the societal level rise with the strength of political and social infrastructure in their ability to reduce conflict.

Accordingly, when the number of people in a group is much larger, i.e. entire cities, the costs of diversity can become much more difficult to manage. For example, heterogeneity can induce costs from conflicting preference sets, communication costs, and social capital costs such as outright racism and prejudice (Alesina, Bar, and Easterly). One tangible implication of such costs is a sub-optimal provision of private and public goods. However, strong political infrastructure can nullify the harmful effects of fractionalization.

Economists, sociologists, and political scientists have contributed vast literature on the impact of diversity on public goods. According to Williams and O’Reilly (1998), the social characterization view posits that individual perspectives are defined by one’s similarities and differences and a characterization of insiders and outsiders. Unless there are measures in place to facilitate coordination, empirical evidence suggests that diversity is more likely to harm group performance. Social capital and trust is greater amongst insiders, implying greater conflict between heterogeneous groups (Fearon and Laitin 1996). Alesina, Bar and Easterly (1999) shows an adverse relationship between the extent of ethnic fragmentation in an economy and level of spending on public goods. Easterly and Levine (1997) find that the underperformance of African nations is attributable to high levels of ethnic fractionalization, resulting in weaker numbers of telephones, percentage of roads paved, efficiency of the electricity network and years of schooling.

The effect of diversity on developing countries can also depend on the magnitude of heterogeneity. Nikolova (2013) finds that the relationship between diversity and entrepreneurship will follow an inverted U-shaped pattern. When the level of cultural heterogeneity is low to medium, its benefits will outweigh the costs, since enforcing inter-group collaboration is easy. However, as the number of religious and linguistic groups increases, the costs of establishing complex institutions outweigh the advantages involving social networks.

Recent literature has found that strong political and economic institutions, such as protection of property, free markets, the rule of law, and a free media, can mitigate and even nullify the harm caused by ethnic fractionalization. Leeson (2005) explains that the legacy of colonization in Africa maintain weak institutions that disrupt trade, hindering economic growth. The negative effect of fractionalization is secondary to the colonial institutions of property law and religious policy. Alesina and La Ferrara (2005) find rich democratic societies work well with diversity in terms of productivity and growth, particularly in the United States.

Diversity and Economic Growth:

Previous research on the role of diversity on productivity has primarily relied on differences in ethnicity and language to measure diversity. Ottaviano (2005) finds a positive effect of linguistic diversity on wages across metropolitan statistical areas in the US. His research indicates that cities with richer linguistic diversity enjoy systematically higher wages and employment density of US-born workers. Audretsch and Feldman (2004) find that diversity across complementary economic activities is more conducive to innovative output than is the specialization. Building on this result, Audretsch (2009) adds that cultural diversity of people and its effect on the level of knowledge form an ideal ecosystem for technology-oriented start-ups.

Florida (2001, 2002) takes a unique approach by creating the bohemian index, a measure of the bohemian concentration for MSAs with the 50 greatest populations. Florida defines a bohemian as an individual practicing an artistic occupation, such as author, designer, musician, composer, actor, painter, sculptor, performer, or dancer. The theoretical relationship between bohemia and entrepreneurship relies on the role of “bohemian” diversity in nurturing cultural and creative milieus. Florida suggests that the presence of alternative communities supports an environment that welcomes innovation and creativity. The results find a positive and significant relationship between the bohemian index and concentrations of high-technology industry. Such ecosystems are more likely to be tolerant of unique ideas and consequently more likely to attract creative and entrepreneurial leaders. However, Florida does not explicitly state a mechanistic relationship between bohemian concentrations and concentrations of start-ups.

By definition, a region with many different worldviews contains a wider variety of preference sets than a homogenously oriented society. But in addition to the relatively greater number of viewpoints, diversity itself also expands the breadth of goods and services. Heterogeneity multiplies possible combinations of ideas and increases the likelihood of creative destruction and innovation. It increases opportunities for ideas to merge, for the study of interdisciplinary fields, and for clashing perspectives to challenge each other’s assumptions. Consequently, new sets of skills become required to produce the new goods and services.

Studying the merging of cultures through trade, Cowen (2002) argues that globalization enhances the range of individual choice and expands the menu of choices available to consumers. It is not merely that the multitude of backgrounds expands individual choices; Cowen suggests that the infusion of cultures inevitably spurs innovation and gives rise to hybrids and new genres. Audretsch and Feldman (1994) studied sectoral diversity and found that specialization of economic activity does not promote innovative output; rather, it is the diversity across complementary economic activities that is more conducive to innovation than is specialization.

DATA DESCRIPTION:

Dependent Variables

The Business Dynamics Statistics (BDS) provides annual measures of business dynamics such as firm openings, firm closings, job creation, and job destruction. The Census Bureau maintains the BDS using data provided from the Business Register, payroll taxes from the Internal Revenue Service, and Annual Survey of Manufacturers. The BDS provides the most comprehensive measure of startup formation and also provides specific counts of firms of age zero to one with nine or fewer employees. In order that coefficients of regression results can be easier to interpret, I use new firms per 10,000 capita to represent the level of startup formation.

One disadvantage of the BDS is that the data does not provide detailed industry information at the MSA level. The inability to filter by industrial sector makes it difficult to assess the level of innovation in cities. In order to more directly address the relationship between heterogeneity and innovation, I will also be using a measure of patents per capita as provided by the United States Patent and Trademarke Office (USPTO).

Explanatory Variables

The ethnic index of fractionalization is the most common method of measuring cultural diversity. Using a person’s place of birth to represent his or her distinct cultural identity, the index ranks regions based on the degree of heterogeneity. The index is equal to zero if the region is completely homogenous and approaches one as diversity increases.

$CDI_i = 1 - \sum_{m=1}^{M_i} s^2_{im}$

s_im is region i’s population share belonging to nationality m and M_i is the number of different nationalities actually present in region i. As Audretsch (2010) explains, this approach to measuring cultural diversity has an unpleasant characteristic because it weights the highest share (e.g. Those born in America) disproportionately high.

In order to account for the distribution of different nationalities within the foreign population, Audretsch suggests the use of an entropy index:, also known as the Theil index of cultural diversity:

$T_i = - \sum_{m=1}^{M_i} s_{im} * ln(s_{im})$

For each region i, the index takes the sum of the product of the shares and log shares of each group in the total population. If all ethnicities are of equal size in a region, the index is equal to ln(1) = 0. As diversity increases, the index value approaches ln(M_i).

There are also variations of the ethnic index of fractionalization that apply the same arithmetic using a different definition of cultural identity. For example, the Linguistic Diversity Index (LDI) is an alternate method of measuring diversity and uses language as a proxy for cultural identity. One key benefit of the LDI is that it can capture cultural identity beyond first-generation immigrants. In contrast, a foreign country of origin is unique to the first generation immigrant. Studies have also used religion to classify cultural identities. Nikolova (2015), for example, uses religious diversity to capture the effect of religious heterogeneity in new firm startups in Central and Eastern Europe.

Ethnic, linguistic, and religious diversity are reasonable measures of cultural diversity. Within the context of the theoretical relationship between diversity and productivity, however, there is room for improvement. The primary benefit of cultural diversity is not simply the presence of different ethnic flavors, but the presence of divergent perspectives, of which ethnic identity is just one. The theoretical relationship between cultural diversity and productivity is also applicable to occupational diversity and educational diversity. In both cases, the fundamental theme of an economic benefit from the presence of varying world views persists. Cultural diversity is a good indication of heterogeneity of perspectives, but cultural diversity within the context of education and occupation provides a stronger measure. To attempt to improve the measurement of heterogeneity, I formulated a new index called the Diversity of Perspectives Index. The index is calculated using the entropy index method:

$DPI_i = - \sum_{m=1}^{M_i} s_{im} * ln(s_{im})$

The new index is similar to the Thiel index; however, m no longer represents just a nationality; rather, each m is a unique combination of gender, nationality, occupation, and area of study. Whereas CDI and LDI would represent a person born in Canada as one identity, the DPI would define a female lawyer born in Canada with a degree in Engineering as a unique identity. In this way, the DPI adds to the traditional calculation of diversity as a measure of the variety of nationalities. The DPI incorporates the mixture and assimilation of different ethnicities and genders.

A correlation matrix of both independent and dependent variables reveals that the CDI, LDI, and Theil index are nearly perfectly correlated to each other. The correlation between the DPI and each of the three alternative measures of diversity is relatively more moderate. With regard to the dependent variables, firms per capita (FPC) and patents per capita (PPC), there is a weak relationship.

IDENTIFICATION STRATEGY:

I estimate two sets of Ordinary Least Squares regressions for each measure of entrepreneurial activity: new firms per capita (FPC) and patents per capita (PPC). The first set tests the relationship between entrepreneurial activity and the Diversity of Perspectives Index (DPI). The second set estimates a multiple linear regression model with both traditional measures of diversity as well as the DPI. The total group of indices will consist of the Cultural Diversity Index, the Linguistic Diversity Index, the Thiel Index, and Diversity of Perspectives Index.

First, I estimate the relationship between the DPI and startup formation. The econometric model has the basic form:

$EA_i = \beta_0 + \beta_1DPI_i + \epsilon_i$

where $EA_i$ is the level of new firm formation in region i. A new firm is defined as a business aged between 0 to 1 years and consisting of fewer than 9 employees. $DPI_i$ is the diversity measure in region i. The error term, $\epsilon_i$ , captures the effect of an incorrect functional form, the effects of omitted variables, and the measurement errors.

Second, I estimate a model with the inclusion of other indices:

$EA_i = \beta_0 + \beta_1DPI_i + \beta_2CDI_i + \beta_3LDI_i + \beta_4T_i + \epsilon_i$

where for region i, CDI is the cultural diversity index, LDI is the linguistic diversity index and T is the Thiel Index.

RESULTS:

Table 1 shows that a higher level of diversity leads to a greater number of new firm formations. Even when CDI, LDI, and Thiel indices are added to the model, the effect of the DPI index on new firm formation remains significant. Column 1 shows that a 1-point increase in the DPI increases the number of new startups per 10,000 capita by 5.544. Similarly, Column 3 shows that a 1-point increase in the DPI leads to an increase of 1.1% share of startups relative to firms of all ages. In both cases, I can reject the null hypothesis that DPI has no significant effect on the startup rate.

Column 2 shows that the coefficient on diversity of perspectives remains positive and significant at the 1 percent level even with the incorporation of CDI, LDI, and Thiel indices as independent variables. Since CDI, LDI, and Thiel indices are strongly correlated to each other, multicollinearity issues between the three traditional measures of cultural diversity reduce the precision of the regression and are likely causes of the negative coefficients for CDI and LDI. However, the three traditional measures of diversity are not strongly correlated to the DPI and do not affect the significance of the coefficient for DPI. The implication is that the diversity of perspectives index contributes to startup formation even when controlling for the effects of single dimensional indices that measure ethnic and linguistic diversity.

In Column 4, the DPI survives the same test using the share of new firms as the independent variable, instead of firms per capita. Again, adding CDI, LDI, and Thiel indices to the model, the coefficient for the DPI remains significant at one percent. There still remain multicollinearity issues between CDI, LDI, and Thiel, which are likely causes of the negative coefficients for LDI and Thiel index. For both firms per capita and share of new firms, the DPI is strongly correlated to startup formation rate in spite of the addition of traditional diversity measures to the model.

TABLE 1:

screen shot 2019-01-06 at 4.34.42 pm — The CDI, LDI, Thiel Index, and DPI are calculated using data taken from the One Percent Public Use Microdata Sample of the 2014 U.S. Census. “FirmsPerCap” is the number of new firms per 10000 capita and data is taken from the Business Dynamics Statics for 2014. A region is “region” is defined as Metropolitan Statistical Area. The 100 largest MSAs in the United States were used in this model.

Table 2 shows that a higher DPI value leads to a greater number of patents per 10,000 capita. In Column 1, the coefficient is positive and significant at the 1-percent level and a 1-point increase in the DPI is associated with an increase of 3.386 patents. However, when the alternative measures of diversity are incorporated into the model in Column 2, the coefficient for DPI is negative and no longer significant. Instead, the coefficient for LDI is very large and significant. Due to multicollinearity issues, however, I cannot conclude that the linguistic diversity is a strong indicator of patents per capita. Additional tests are required to determine the strength of the relationship between linguistic diversity and patents.

Table 2:

screen shot 2019-01-06 at 4.34.59 pm — The CDI, LDI, Thiel Index, and DPI are calculated using data taken from the 1% Public Use Microdata Sample of the 2014 U.S. Census. “PatentsPerCap” is the number of technology patents per 10000 capita and data is taken from the United States Patent and Trademark Office for 2014. “Region” is defined as Metropolitan Statistical Area. The 100 largest MSAs in the United States were used in this model.

Conclusion:

Using a newly constructed measure of diversity, the Diversity of Perspectives Index, this paper finds that an increase in diversity leads to growth in the creation of startups. The results are consistent even with the addition of traditional measures of diversity, such as the cultural diversity index, linguistic diversity index, and the Thiel index. The implication is that greater variety in the number of ethnicities working in various professions with different educational backgrounds leads to a higher propensity to start new firms.

One key limitation of this study is the restricted availability of characteristics that can be used to determine a “perspective”. The diversity of perspectives index was created using the One Percent Public Use Microdata Sample of the 2014 U.S. Census. For this reason, the index was limited to nationality, gender, field of study, and occupation. If the data were available, the inclusion of other identity characteristics such as political affiliation and religious practice into the index calculation could provide a stronger or perhaps weaker relationship to startup formation.